- Задания девятой олимпиады по математике осень 2021 5 класс | систематика
- Задания и ответы пригласительного этапа 2021 вош:
- Поделиться
- Пригласительный этап вош 2021 по математике 3 класс задания:
- Пригласительный этап вош 2021 по математике 4 класс задания:
- Пригласительный этап вош 2021 по математике 5 класс задания:
- Пригласительный этап вош 2021 по математике 6 класс задания:
- Школьный этап 2021 олимпиады по математике 4-11 класс всош
Задания девятой олимпиады по математике осень 2021 5 класс | систематика
Задача №1
Автор: Вольфсон Георгий
Назовем число красивым, если его сумма цифр делится на 17 без остатка.
Существует ли два подряд идущих красивых числа?
Задача №2
Автор: Вольфсон Георгий
Придумайте наибольшее натуральное число, меньшее миллиона, все слова при записи которого по-русски, начинаются на одну и ту же букву.
Задача №3
Автор: Данченко Оксана
На острове живут рыцари и лжецы. Рыцари всегда говорят только правду, лжецы – всегда лгут.
6 шариков, 5 из которых белые и 1 черный, раздали поровну троим островитянам.
Каждый из них про свой набор шариков высказал одно утверждение: «Черных меньше, чем белых», «Черных не меньше, чем белых», «Черных и белых поровну».
Какое наибольшее число рыцарей могло быть среди них?
Задача №4
Автор: Данченко Оксана
От шахматной доски Петя отпилил поле b7, а Вася поле h2.
У кого из мальчиков больше способов замостить доску трехклеточными уголками без дыр и наложений?

Задача №5
Автор: Данченко Оксана
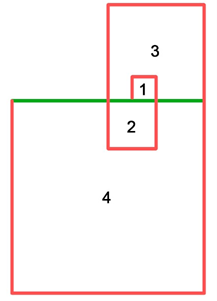
На веревку длиной 24 метра упала согнутая проволока. При этом образовалось 4 квадрата.
Найдите длину проволоки, если известно, что площадь каждого следующего квадрата в 4 раза больше, чем предыдущий.
(На рисунке верёвка обозначена зелёным, проволока красным)
Задача №6
Автор: Данченко Оксана
В семье гномов заведено, что гном своему более молодому родственнику всегда врет, а более старшему обязан говорить правду. 2021 гном встал в шеренгу. Каждый (кроме крайне правого) своему правому соседу сказал «я твой отец». Может ли каждый (кроме крайне левого) своему левому соседу сказать «ты не самый старый из нас»?
Задача №7
Автор: Данченко Оксана
На мониторе высвечивался ряд натуральных чисел (не обязательно идущих подряд). Вася запустил последовательно 4 вируса. «Тьма» уничтожал все числа кратные 3. «Ужас» уничтожал все числа, делящиеся на 5 с остатком 2. «Мрак» все числа которые были больше 17, но не превосходящие 33. А «Жуть» все числа кратные 4. Когда учитель подошел к компьютеру, он выяснил, что «Тьма» удалила числа – 9, 18, 90, 99. «Ужас» — 2, 7, 17, 62, 67. «Мрак» — 22, 23, 25, 29.
А «Жуть» — 16, 32, 36, 44 и 88. Определите в какой последовательности Вася мог запустить эти вирусы.
Задача №8
Автор: Овчинников Михаил
Почему в отражении в зеркале право и лево меняется местами, а верх и низ не меняются?
Задания и ответы пригласительного этапа 2021 вош:
Пригласительный школьный этап 2021 всероссийская олимпиада школьников задания и ответы
Поделиться
Задания и ответы пригласительного этапа 2021 года ВОШ (Сириус) по математике для 3, 4, 5, 6 класса всероссийской олимпиады школьников, дата проведения онлайн олимпиады: 12.05.2021 (12 мая 2021 год).
Пригласительный этап вош 2021 по математике 3 класс задания:
1)Вася на следующий день после своего дня рождения сказал: «Жаль, что мой день рождения в этом году не в субботу, ведь в этом случае ко мне бы пришло больше гостей! Но суббота будет послезавтра…» В какой день недели у Васи был день рождения?
2)Кубик повернули вокруг указанной оси так, что отмеченная грань повернулась указанным образом. А в вершину с каким номером перешла точка A?
3)Несколько букв А и несколько букв Б сидели на трубе. После того, как несколько А упало и несколько Б пропало, на трубе остались всего три буквы и между ними произошёл следующий диалог: Первая буква: «Буква Б среди нас одна.» Вторая буква: «Я здесь одна такая буква.
4)Замените картинки на цифры так, чтобы суммы по столбцам и по строкам были равны указанным. Одинаковые картинки соответствуют одинаковым цифрам, а разные — разным. Какое число после замены картинок на цифры получится под таблицей?
5)Ваня написал на доске число 1347 . — Смотри! — заметил Петя. — В этом числе каждая из двух последних цифр равна сумме двух предыдущих. — Точно! — согласился Вася. — А сможешь написать самое большое четырёхзначное такое число? Помогите Васе справиться с Петиным заданием.
6)Петя умеет рисовать всего 4 вещи: солнце, мячик, помидор и банан. Зато крайне правдоподобно! Сегодня он нарисовал несколько вещей, среди которых ровно 19 жёлтых, 22 круглых и 17 съедобных. Какое наибольшее количество мячиков он мог нарисовать?
7)Катя коротает время, пока родители работают. На листке бумаги она задумчиво в два ряда нарисовала Чебурашек (в каждом ряду оказался нарисован хотя бы один Чебурашка). Потом, подумав, между каждыми двумя соседними Чебурашками в ряду она нарисовала по крокодилу Гене.
А затем слева от каждого Чебурашки — по старухе Шапокляк. И напоследок между каждыми двумя персонажами в ряду она нарисовала по Кракозябре. Внимательно посмотрев на рисунок, она поняла, что красиво получились у неё только Кракозябры, и яростно стёрла всех остальных. В итоге родители увидели два ряда Кракозябр: всего 29 штук. Сколько Чебурашек было стёрто?
8)У берега реки покачивался небольшой плот. К берегу подошли 5 мышат весом по 60 г, 3 крота весом по 90 г и 4 хомячка весом по 120 г. Какое минимальное количество граммов должен выдерживать плот, чтобы все звери смогли на нём переправиться на другой берег, возможно, за несколько ходок «туда сюда»? Плот не может передвигаться по реке без гребца.
Пригласительный этап вош 2021 по математике 4 класс задания:
1)Поставьте в соответствие каждой букве цифру 1,2,3,4,5 так, чтобы выполнялись все неравенства. К < Н < И < Ж > К > А Разным буквам должны соответствовать разные цифры. В качестве ответа запишите число КНИЖКА.
2)Вторник будет через пять дней после позавчера. А какой день недели будет завтра?
3)Сколько на данной картинке существует прямоугольников со сторонами, идущими по линиям сетки? (Квадрат также является прямоугольником.)
4)Четыре девочки: Катя, Оля, Лиза и Рита — встали в круг в некотором порядке. На них были платья разных цветов: розовое, зелёное, жёлтое и голубое. Известно, что: на Оле было не розовое и не голубое платье; девочка в зелёном платье стоит между Ритой и девочкой в жёлтом; Катя не в зелёном и не в голубом платье; Лиза стоит между Катей и девочкой в розовом платье. Кто во что одет?
5)Напишите наибольшее девятизначное число, в котором встречаются все чётные цифры. (Чётные цифры: 0,2,4,6,8.)
6)Часть цифр в прямоугольнике уже расставлена. Расставьте на оставшихся местах цифры так, чтобы: сумма цифр в каждом столбце была одинаковой; сумма цифр в каждой строчке была одинаковой; сумма цифр в красных клетках была равна сумме цифр в любой строчке. В качестве ответа введите трёхзначное число ABC (т. е. составленное из цифр, оказавшихся на местах букв A, B, C).
7)У берега реки стоит Белоснежка, а рядом с ней 7 гномов в следующем порядке слева направо: Весельчак, Соня, Умник, Чихун, Ворчун, Скромник и Простачок. У берега качается лодка, вмещающая только 3 гномов и Белоснежку. Белоснежка единственная умеет грести.
8)Если в числе 79777 зачеркнуть цифру 9, получится число 7777. Сколько существует различных пятизначных чисел, из которых можно получить 7777, зачеркнув одну цифру?
Пригласительный этап вош 2021 по математике 5 класс задания:
1)Саша выписал на доску все двузначные числа, делящиеся на 6, а затем стёр те из них, которые оканчиваются не на 4. Какое наибольшее число в итоге оказалось написано на доске?
2)На столе лежат апельсин, банан, мандарин, персик и яблоко. Их веса равны 100 г, 150 г, 170 г, 200 г, 280 г, но неизвестно, какой фрукт сколько весит. Известно, что: персик легче апельсина; мандарин тяжелее банана, но легче персика; яблоко легче мандарина; банан и мандарин вместе тяжелее апельсина. Какой фрукт сколько весит?
3)На стене висят часы с кукушкой. Когда начинается новый час, кукушка говорит «ку-ку» количество раз, равное числу, на которое показывает часовая стрелка (например, в 19:00 «ку-ку» звучит 7 раз). Как-то утром Максим подошёл к часам, когда на них было 9:05.
4)На дискотеку по случаю окончания учебного года пришло в два раза больше мальчиков, чем девочек. Маша посчитала, что девочек, кроме неё самой, на дискотеке на 9 меньше, чем мальчиков. Сколько мальчиков пришло на дискотеку?
5)Из клетчатого квадрата 7×7 вырезали голубые треугольники. Чему равна площадь оставшейся фигуры? Длина стороны каждой клетки равна 1 см. Ответ дайте в квадратных сантиметрах.
6)На доске написано одно трёхзначное число и два двузначных. Сумма чисел, в записи которых есть семёрка, равна 214. А сумма чисел, в записи которых есть тройка, равна 75. Найдите сумму всех трёх чисел.
7)Вася хочет расставить в квадратики числа от 1 до 6 (каждое — по одному разу) так, чтобы выполнялось следующее условие: если два квадратика соединены, то в том, который выше, число больше. Сколько существует способов это сделать?
8)В стране 100 городов: 30 из них находятся в горной части страны, а 70 — в равнинной. В течение трёх лет между городами устанавливали авиасообщение. Каждый год в стране открывалось 50 новых авиарейсов: все города случайным образом разбивались на 50 пар, и между городами из одной пары открывался рейс.
Пригласительный этап вош 2021 по математике 6 класс задания:
1)Маша расставила числа от 1 до 16 в клетки таблицы 4×4 так, чтобы любые два числа, отличающиеся на единицу, стояли в соседних по стороне клетках. А Саша стёр все числа, кроме 1 , 4, 9 и 16. Какое число стояло в клетке с вопросом?
2)Для приготовления одной порции салата требуются 2 огурца, 2 помидора, 75 грамм брынзы и 1 перец. На складе ресторана есть 92 перца, 6,6 кг брынзы, 180 помидоров и 181 огурец. Сколько порций получится?
3)Витя и его мама одновременно вышли из дома и пошли в противоположные стороны с одинаковой скоростью: Витя — в школу, а мама — на работу. Через 16 минут Витя понял, что у него нет ключей от дома, а вернётся из школы он раньше мамы, поэтому он стал догонять её, увеличив скорость в пять раз. Через сколько минут с того момента, как он понял, что надо забрать ключи, Витя догонит маму?
4)Алексей, Борис, Вениамин и Григорий подозреваются в ограблении банка. Полиции удалось выяснить следующее: если Алексей невиновен, то Вениамин виновен, а Борис невиновен; если Григорий виновен, то Борис и Вениамин невиновны; если Алексей виновен, то Вениамин тоже виновен;
5)В парке проложены дорожки, как показано на рисунке. Двое рабочих начали их асфальтировать, одновременно стартовав из точки A. Они укладывают асфальт с постоянными скоростями: первый — на участке A−B−C, второй — на участке A−D−E−F−C. В итоге они закончили работу одновременно, потратив на неё 15 часов. Известно, что второй работает в 1,2 раза быстрее первого. Сколько минут второй укладывал асфальт на участке DE ?
6)С дерева сорвали несколько апельсинов (не обязательно равной массы). Когда их взвесили, то оказалось, что масса любых трёх апельсинов, взятых вместе, составляет меньше 4% от суммарной массы остальных апельсинов. Какое наименьшее количество апельсинов могло быть сорвано?
7)Петя загадывает четырёхзначное число вида 19∗∗ . Вася последовательно проверяет, делится ли загаданное Петей число на 1,3,5,7,9,11 , и если делится, то Вася платит Пете 1,3,5,7,9 или 11 рублей соответственно. Например, за число 1900 Вася заплатил бы Пете 1 5=6 рублей. Какое наибольшее количество рублей может получить Петя?
8)Существует ровно 120 способов закрасить пять клеток в таблице 5×5 так, чтобы в каждом столбце и в каждой строке была закрашена ровно одна клетка. Существует ровно 96 способов закрасить пять клеток в таблице 5×5 без угловой клетки так, чтобы в каждом столбце и в каждой строке была закрашена ровно одна клетка.
Школьный этап 2021 олимпиады по математике 4-11 класс всош
1)На девяти карточках написаны числа от 1 до 9 (каждое — по одному разу). Эти карточки выложили в ряд так, что нет трёх подряд лежащих карточек, на которых числа идут по возрастанию, а также нет трёх подряд лежащих карточек, на которых числа идут по убыванию. Затем три карточки перевернули числом вниз, как показано на рисунке. Какие числа на них написаны?
2)Найдите наименьшее число, у которого все цифры различны, а сумма всех цифр равна 32.
3)Женя нарисовал квадрат со стороной 3 см, а затем одну из этих сторон стёр. Получилась фигура в виде буквы «П». Учительница попросила Женю расставить точки вдоль этой буквы «П», начиная с края, так, чтобы следующая точка была на расстоянии 1 см от предыдущей, как показано на рисунке, а затем посчитать, сколько получилось точек. Точек у него получилось 10.
4)Лев Алекс решил посчитать полоски на зебре Марти (чёрные и белые полоски чередуются). Оказалось, что чёрных полосок на одну больше, чем белых. Также Алекс заметил, что все белые полоски одинаковой ширины, а чёрные бывают широкие и узкие, причём всего белых полосок на 7 больше, чем широких чёрных. Сколько всего у Марти узких чёрных полосок?
5)Хулиган Дима выложил из 38 деревянных зубочисток конструкцию в виде прямоугольника 3 × 5. Затем он одновременно поджёг два соседних угла этого прямоугольника, отмеченных на рисунке. Известно, что одна зубочистка сгорает за 10 секунд. За сколько секунд сгорит вся эта конструкция?
6)Разведчик хочет передать сообщение, состоящее из нескольких написанных в ряд букв А, Б и В. Для секретности каждая буква кодируется: буква А заменяется на 011, буква Б — на 01, буква В — на 10. Используя данную кодировку, разведчик получил код 011011010011.
Появилась информация, что данную кодировку расшифровали, в связи с чем разведчику придётся использовать запасную кодировку. В ней буква А заменяется на 21, буква Б — на 122, буква В — на 1. Какой код получится у данного сообщения в новой кодировке?
7)Школьники Александр, Борис, Сергей, Дарья и Елена с понедельника по пятницу посещали занятия хора. Известно, что: • в каждый из пяти дней ровно трое из школьников присутствовали, а ровно двое отсутствовали; • никто из школьников не отсутствовал два дня подряд и никто не присутствовал три дня подряд;
8)На рисунке изображена схема дорог между домами пяти ребят. От Аси до Гали кратчайшее расстояние по дорогам12 км, от Гали до Бори —10 км, от Аси до Бори — 8 км, от Даши до Гали — 15 км, от Васи до Гали — 17 км. Сколько километров составляет кратчайшее расстояние по дорогам от Даши до Васи?
9)В некотором месяце некоторого года ровно 5 пятниц. При этом первый и последний день этого месяца — не пятницы. Каким днём недели является 12-е число месяца?
10)За круглый стол рассадили несколько человек так, что между соседними людьми расстояния одинаковые. Одному из них дали табличку с номером 1 и дальше по часовой стрелке раздали всем таблички с номерами 2, 3 и т. д. Человек с табличкой с номером31 заметил, что от него до человека с табличкой с номером 7 такое же расстояние, как и до человека с табличкой с номером 14. Сколько всего людей сели за стол?
11)На рисунке изображён план системы дорог некоторого города. В этом городе 8 прямых улиц, а 11 перекрёстков названы латинскими буквами 𝐴, 𝐵, 𝐶, … , 𝐽, 𝐾. На некоторые три перекрёстка надо поставить по полицейскому так, чтобы на каждой из 8 улиц стоял хотя бы один полицейский.
На какие именно три перекрёстка надо поставить полицейских? Достаточно указать хотя бы один подходящий вариант расположения. Все улицы направлены вдоль прямых линий. Горизонтальные улицы: 𝐴−𝐵−𝐶−𝐷, 𝐸−𝐹−𝐺, 𝐻−𝐼−𝐽−𝐾. Вертикальные улицы: 𝐴−𝐸−𝐻, 𝐵−𝐹−𝐼, 𝐷−𝐺−𝐽. Наклонные улицы: 𝐻−𝐹−𝐶, 𝐶−𝐺−𝐾.
12)Директор школы, завхоз и родительский комитет, не договорившись друг с другом, купили по ковру для школьного актового зала размером 10 × 10. Подумав, что же делать, они решили положить все три ковра так, как показано на картинке: первый ковёр 6×8 — в один угол, второй ковёр 6×6 — в противоположный угол и третий ковёр 5×7 — в один из оставшихся углов (все размеры указаны в метрах). Найдите площадь части зала, накрытой коврами в три слоя (ответ дайте в квадратных метрах).
13)На кружки по математике записалось несколько школьников. Их хотят распределить по группам равномерно — таким образом, чтобы количество учеников в любых двух группах отличалось не более чем на 1. В результате такого равномерного деления получилось 6 групп, среди которых ровно 4 группы по 13 учеников. Сколько всего могло быть школьников? Укажите все возможные варианты.
14)Несколько камней разложены в 5 кучек. Известно, что • в пятой кучке камней в шесть раз больше, чем в третьей; • во второй кучке камней вдвое больше, чем в третьей и пятой вместе взятых; • в первой кучке камней втрое меньше, чем в пятой, и на 10 меньше, чем в четвёртой; • в четвёртой кучке камней в два раза меньше, чем во второй. Сколько всего суммарно камней в этих пяти кучках?
15)После чемпионата мира по хоккею три журналиста написали статью о сборной Германии — каждый для своей газеты. • Первый написал: «Сборная Германии за весь чемпионат забила больше 10, но меньше 17 шайб». Второй: «Сборная Германии забила больше 11, но меньше 18 шайб за весь чемпионат». • Третий:
16)Внутри большого треугольника периметра 120 провели несколько отрезков, которые разделили его на девять меньших треугольников, как показано на рисунке. Оказалось, что периметры всех девяти маленьких треугольников равны между собой. Чему они могут быть равны? Укажите все возможные варианты. Периметр фигуры — сумма длин всех её сторон.
17)Пять последовательных натуральных чисел написаны в ряд. Сумма трёх самых маленьких из них равна 60. Чему равна сумма трёх самых больших?
18)Аркадий, Борис, Вера, Галя, Даня и Егор встали в хоровод. • Даня встал рядом с Верой, справа от неё, • Галя встала напротив Егора, • Егор встал рядом с Даней, • Аркадий и Галя не захотели стоять рядом. Кто стоит рядом с Борисом?
19)В клетках таблицы 4 × 4 расставлены числа 1, 2, 3, 4 так, что • каждое из чисел встречается в каждой строке и в каждом столбце; • во всех четырёх частях, изображённых на рисунке, суммы чисел равны. По двум числам на рисунке определите, в каких клетках стоят двойки.
20)Миша летом на даче изготовил себе самодельный дартс. Круглая доска разделена окружностями на несколько секторов — в неё можно кидать дротики. За попадание даётся столько очков, сколько написано в секторе, как указано на рисунке. Миша кидал 3 раза по 8 дротиков.
21)Несколько одноклассников вместе съели торт. Лёша съел больше всех — 1 11 от всего торта, а Алёна — меньше всех — 1 14 от всего торта. Сколько одноклассников ели торт? Укажите все возможные варианты.
22)На острове живут рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. Однажды 65 жителей острова собрались на заседание. Все они по очереди сделали заявление: «Среди сделанных ранее заявлений истинных ровно на 20 меньше, чем ложных». Сколько рыцарей было на этом заседании?
23)Аня расставляет камешки на песке. Сначала она поставила один камень, потом добавила камешки, чтобы получился пятиугольник, затем сделала из камешков внешний большой пятиугольник, после этого ещё один внешний пятиугольник и т. д., как на рисунке.
24)Крест, состоящий из двух одинаковых больших и двух одинаковых маленьких квадратов, поместили внутрь ещё большего квадрата. Вычислите в сантиметрах сторону самого большого квадрата, если площадь креста — 810 см2 .
25)Саша и Ваня играют в игру. Саша задаёт Ване вопросы. Если Ваня отвечает на вопрос правильно, то Саша даёт ему 7 конфет. Если же Ваня отвечает неправильно, то он даёт Саше 3 конфеты. После того, как Саша задал 50 вопросов, оказалось, что у каждого из них столько же конфет, сколько было в начале. На сколько вопросов Ваня ответил правильно?
26)На День учителя благодарные ученики подарили Егору Сергеевичу несколько железнодорожных билетов, чтобы он совершил путешествие по России. Билеты были для проезда между следующими парами городов: • Санкт-Петербург и Тверь, • Ярославль и Нижний Новгород, • Москва и Казань, • Нижний Новгород и Казань, • Москва и Тверь, • Москва и Нижний Новгород.
27)В клетках квадрата расставили числа так, что суммы чисел в каждой вертикали, горизонтали и каждой диагонали из трёх клеток равны. Затем некоторые числа скрыли. Чему равна сумма чисел в двух закрашенных клетках?
28)Маша и Оля купили в магазине много одинаковых ручек для нового учебного года. Известно, что одна ручка стоит целое число рублей, большее 10. Маша купила ручек ровно на 357 рублей, а Оля — ровно на 441 рубль. Сколько суммарно ручек они купили?
29)В каждую комнату отеля можно поселить не более 3 человек. Менеджер отеля знает, что скоро приедет группа из 100 футбольных фанатов, которые болеют за три разные команды. В одну комнату можно селить только мужчин или только женщин; также нельзя вместе селить фанатов разных команд. Сколько комнат нужно забронировать, чтобы точно расселить всех фанатов?
30)В классе учатся 25 школьников, каждый из которых либо отличник, либо хулиган. Отличники всегда говорят правду, а хулиганы всегда врут. Однажды 5 учеников этого класса сказали: «Если я перейду в другой класс, то среди оставшихся учеников будет больше половины хулиганов».
31)Числа от 1 до 200 в произвольном порядке расставили на окружности так, что расстояния между рядом стоящими на окружности числами одинаковы. Для любого числа верно следующее: если рассмотреть 99 чисел, стоящих от него по часовой стрелке, и 99 чисел, стоящих от него против часовой стрелки, то в обеих группах будет поровну чисел, которые меньше его. Какое число стоит напротив числа 113?
32)На прямоугольном листе бумаги нарисовали картинку в форме «креста» из двух прямоугольников 𝐴𝐵𝐶𝐷 и 𝐸𝐹𝐺𝐻, стороны которых параллельны краям листа. Известно, что 𝐴𝐵 = 9, 𝐵𝐶 = 5, 𝐸𝐹 = 3, 𝐹𝐺 = 10. Найдите площадь четырёхугольника 𝐴𝐹𝐶𝐻.
33)На клавиатуре компьютера Пети неисправна одна клавиша с некоторой цифрой (все остальные клавиши работают хорошо). Неисправная клавиша срабатывает только на каждое второе нажатие. Например, в случае неисправной клавиши «2» при вводе числа 12125252 получится число 112552.
34)В чате учеников одной из школ проходило голосование: «В какой день проводить дискотеку: 22 или 29 октября?» На графике изображено, как голоса распределились спустя час после начала голосования. Затем в голосовании приняли участие ещё 80 человек, которые голосовали только за 22 октября.
35)В классе учатся 29 школьников: несколько отличников и несколько хулиганов. Отличники всегда говорят правду, а хулиганы всегда врут. Все ученики этого класса сели за круглый стол. • Несколько учеников сказали: «Рядом со мной ровно один хулиган».
36)Точки 𝐷 и 𝐸 отмечены соответственно на сторонах 𝐴𝐶 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 так, что 𝐴𝐷 = 𝐸𝐶. Оказалось, что 𝐵𝐷 = 𝐸𝐷, ∠𝐵𝐷𝐶 = ∠𝐷𝐸𝐵. Найдите длину отрезка 𝐴𝐶, если известно, что 𝐴𝐵 = 7 и 𝐵𝐸 = 2.
37)На доске были написаны числа 1, 2, 3, … , 235. Петя стёр несколько из них. Оказалось, что среди оставшихся чисел никакое не делится на разность никаких двух других. Какое наибольшее количество чисел могло остаться на доске?
38)В таблице 3 × 3 расставлены действительные числа. Оказалось, что произведение чисел в любой строке и любом столбце равно 10, а произведение чисел в любом квадрате 2 × 2 равно 3. Найдите число, стоящее в центральной клетке.
39)На рисунке изображены два равных треугольника: 𝐴𝐵𝐶 и 𝐸𝐵𝐷. Оказалось, что ∠𝐷𝐴𝐸 = ∠𝐷𝐸𝐴 = 37∘ . Найдите угол 𝐵𝐴𝐶.
40)Сколькими способами можно покрасить все натуральные числа от 1 до 200 в красный и синий цвета так, чтобы никакая сумма двух различных одноцветных чисел не равнялась степени двойки?
41)На острове живут красные, жёлтые, зелёные и синие хамелеоны. • В пасмурный день либо один красный хамелеон меняет окрас на жёлтый цвет, либо один зелёный хамелеон — на синий цвет. • В солнечный день либо один красный хамелеон меняет окрас на зелёный цвет, либо один жёлтый хамелеон — на синий цвет.
42)У Дениса есть карточки с числами от 1 до 50. Сколько существует способов выбрать две карточки так, чтобы разность чисел на карточках равнялась 11, а произведение делилось на 5? Порядок выбранных карточек не важен: например, способ выбора карточек с числами 5 и 16, а также способ выбора карточек с числами 16 и 5 — это один и тот же способ.
43)Торговцы Андрей и Борис купили по 60 мешков картошки у одного и того же фермера. Все мешки стоили одинаково. Андрей продал все свои мешки, увеличив их цену на 100%. Борис же сначала увеличил цену на 60%, а когда продал 15 мешков, увеличил цену ещё на 40% и продал остальные 45 мешков. Оказалось, что Борис заработал на 1200 рублей больше Андрея. Сколько рублей стоил один мешок картошки у фермера?
44)Через вершину 𝐴 прямоугольника 𝐴𝐵𝐶𝐷 проведена прямая ℓ, как изображено на рисунке. Из точек 𝐵 и 𝐷 опущены перпендикуляры 𝐵𝑋 и 𝐷𝑌 на прямую ℓ. Найдите длину отрезка 𝑋𝑌, если известно, что 𝐵𝑋 = 4, 𝐷𝑌 = 10, 𝐵𝐶 = 2𝐴𝐵.
45)У Леонида есть белый клетчатый прямоугольник. Сначала он покрасил в серый цвет все столбцы через один, начиная с самого левого, а затем все строки через одну, начиная с самой верхней. Все клетки, примыкающие к границе прямоугольника, оказались закрашены.
46)В треугольнике 𝐴𝐵𝐶 известны углы ∠𝐵 = 30∘ и ∠𝐴 = 90∘ . На стороне 𝐴𝐶 отмечена точка 𝐾, а на стороне 𝐵𝐶 — точки 𝐿 и 𝑀 так, что 𝐾𝐿 = 𝐾𝑀 (точка 𝐿 лежит на отрезке 𝐵𝑀). Найдите длину отрезка 𝐿𝑀, если известно, что 𝐴𝐾 = 4, 𝐵𝐿 = 31, 𝑀𝐶 = 3.
47)В школьном шахматном турнире участвовали 4 человека: Андрей, Ваня, Дима и Саша. Каждый сыграл дважды с каждым своим соперником. В каждой игре за победу давалось 1 очко, за ничью — 0,5 очка, за поражение — 0 очков. Известно, что по окончании турнира • все ребята набрали разное количество очков;
48)Целые числа 𝑛 и 𝑚 удовлетворяют неравенствам 3𝑛 − 𝑚 < 5, 𝑛 𝑚 > 26, 3𝑚 − 2𝑛 < 46. Чему может равняться 2𝑛 𝑚? Укажите все возможные варианты.
49)Найдите наибольшее 12-значное число 𝑁, удовлетворяющее двум следующим условиям: • В десятичной записи числа 𝑁 шесть цифр «4» и шесть цифр «7»; • В десятичной записи числа 𝑁 никакие четыре подряд идущие цифры не образуют число «7444».
50)На окружности по часовой стрелке расположены точки𝐴, 𝐵, 𝐶, 𝐷, 𝐸, 𝐹, 𝐺, как изображено на рисунке. Известно, что 𝐴𝐸 — диаметр окружности. Также известно, что ∠𝐴𝐵𝐹 = 81∘ , ∠𝐸𝐷𝐺 = 76∘ . Сколько градусов составляет угол 𝐹𝐶𝐺?
51)Лёша разрезал куб 𝑛 × 𝑛 × 𝑛 на 153 меньших кубика. Причём у всех кубиков, кроме одного, длина ребра равна 1. Найдите 𝑛.
52)В классе учатся 𝑁 школьников: несколько отличников и 8 хулиганов. Отличники всегда говорят правду, а хулиганы всегда врут. Однажды все ученики этого класса сели за круглый стол, и каждый из них заявил всем остальным: «Как минимум треть из вас — хулиганы!
» Чему может быть равно 𝑁? Укажите все возможные варианты. У Вики есть 60 карточек с числами от 1 до 60. Она хочет разбить все карточки на пары так, чтобы во всех парах получался один и тот же модуль разности чисел. Сколько существует способов так сделать?
53)В прямоугольном треугольнике 𝐴𝐵𝐶 с прямым углом 𝐴 проведена высота 𝐴𝐻. Окружность, проходящая через точки 𝐴 и 𝐻, пересекает катеты 𝐴𝐵 и 𝐴𝐶 в точках 𝑋 и 𝑌 соответственно. Найдите длину отрезка 𝐴𝐶, если известно, что 𝐴𝑋 = 5, 𝐴𝑌 = 6, 𝐴𝐵 = 9.


