Олимпиада по математике 5 класс
Задача № 1
Выразите числа 5, 30 и 55, используя четыре цифры 5, знаки арифметических действий и скобки.
Задача № 2
В гимназии 33 учебных кабинета, в 2/3 кабинетах стоят по 12 парт, в остальных по 13.
Около каждой парты стоит по 2 стула. 50% всех стульев имеют по 3 ножки, остальные по 4.
Каждая парта, кроме 7, имеет по 4 ножки, а эти 7 парт по 6.
Столько всего ножек у парт и стульев в учебных кабинетах гимназии?
Задача № 3
Нюша , Бараш, Копатыч и Лосяш играли с мячами синим, зелёным, жёлтым и красным.
Каким из мячей играл каждый из них, если мяч Бараша не синий, у Нюши не синий и не красный,
а у Копатыча желтый мяч?
Задача № 4
В сказочном озере плавает сказочная лилия.
Эта лилия за сутки вдвое увеличивает свои размеры и полностью заполняет озеро за 137 суток.
За какое время заполнят озеро две сказочные лилии?
Задача № 5
Задуманное число добавили к числу, большему его на единицу.
Затем из суммы вычли число, на единицу меньшее задуманного.
В итоге получилось 23. Какое число было задумано?
Задача № 6
Какое наименьшее 10-значное число можно получить, по-разному записывая
шесть чисел 315, 41, 6, 7, 63 и 2 одно за другим?
Задача № 7
Две бутылки A и B заполнены водой.
Сначала 1/4 воды из A перелили в B , а затем 1/3 воды из B перелили в A,
после чего количество воды в них сравнялось.
Найдите первоначальное отношение количества воды в этих бутылках.
Задача № 8
В некотором месяце три воскресенья пришлись на чётные числа.
Каким днём недели могло быть 22 число этого месяца?
Задача № 9
Оттолкнувшись левой ногой, Кенгуру прыгает на 2 метра, правой – на 4, а обеими – на 7.
Какое наименьшее число таких прыжков нужно сделать, чтобы набрать в точности 300 метров?
Задача № 10
Найдите натуральное число N , для которого N 53 и N-36 –полные квадраты.
Задача № 11
Из квадрата со стороной 100 вырезали квадрат со стороной 80.
Оставшийся кусок разрезали на единичные квадратики, из которых Павел хочет сложить новый квадрат.
Чему будет равна его сторона?
Задача № 12
Девочка заменила каждую букву в своём имени её номером в русском алфавите
и получила 2022533.
Как её зовут?
Задача № 13
В букете 11 цветов, причём 5 из них – красные, а 6 – розы.
Какое число белых гвоздик может быть в букете?
Задача № 14
Какое наименьшее 10-значное число можно получить, по-разному записывая шесть чисел:
316, 21, 6, 7, 83, 3 – одно за другим?
Задача № 15
В некотором месяце три понедельника пришлись на нечётные числа.
Каким днём недели могло быть 21 число этого месяца?
Задача № 16
Оттолкнувшись левой ногой, Заяц прыгает на 40 сантиметров, правой – на 50, а обеими – на 95.
Какое наименьшее число таких прыжков нужно сделать, чтобы набрать в точности 300 метров?
Задача № 17
Из квадрата со стороной 100 тетрадных клеточек вырезали квадрат со стороной 80.
Оставшийся кусок разрезали на единичные квадратики (это можно сделать),
из которых Андрей хочет сложить новый квадрат.
Чему будет равна его сторона?
Задача № 18
Вычислите: 1. 180 * 94 – 47700 : 45 4946 2. 86 * 170 – 5793 72800 : 35
Задача № 19
Найдите объём прямоугольного параллелепипеда, измерения которого равны 4м, 3м и 5м.
Задача № 20
Найдите площадь поверхности и объём куба, ребро которого равно 6дм.
Во сколько раз уменьшится площадь поверхности и во сколько раз – объём куба,
если его ребро уменьшить вдвое?
Олимпиада по математике 5 класс | систематика
Победители олимпиады по математике для первого класса получают дипломы, футболки и другие ценные призы
Олимпиадные задания, ответы и решения по предмету математика для учащихся 5-9 классов (школьный этап)
Муниципальное
бюджетное общеобразовательное учреждение
«Лянторская средняя общеобразовательная
школа №4»
Олимпиадные
задания, ответы и решения
по
предмету математика
для
учащихся 5-9 классов
(школьный
этап)
Пивоварова
Татьяна Геннадьевна,
учитель
математики
Задания
5
класс
1. Вы
видите три числа, подписанных одно под
другим:
111
777
999
Надо
зачеркнуть шесть цифр так, чтобы
оставшиеся числа составили в сумме 20.
2.
Расшифруйте запись: О Х О Х О
А Х А Х А
А Х А Х А Х
3. Имеются
два сосуда вместимостью 17 литров и 5
литров. Как с помощью этих сосудов налить
из водопроводного крана 13 литров воды?
4. Хвост
рыбы весит 4 кг, Голова весит столько,
сколько хвост и половина туловища, а
туловище – столько, сколько голова и
хвост. Сколько весит вся рыба?
Ответы
и решения.
5
класс
1. Ответ:
011
000
009
020
2. Ответ:
90909 10101 = 101010.
2.Решение.
Решение задачи задаётся числовым
выражением:
5 – (17 – 5 – 5 – 5) 5 5.
4. Ответ:
32 кг.
Решение.
Хвост (Х). Голова (Г). Туловище (Т).
Х=4кг;
Г =4кг 0,5Т; Т = Г 4кг. Г = 4кг 0,5(Г 4кг);
2Г =
8кг Г 4кг; Г = 12кг; Т = 16кг.
Масса
рыбы: 4 12 16 = 32(кг).
Ответ:
32 кг.
6
класс
Задания
1.
Расшифруйте запись: В А Г О Н
В А Г О Н
С О С Т А В
2.
Когда внук спросил у дедушки, сколько
ему лет, дед ответил: «Если я проживу
ещё половину того, что я прожил, да ещё
1 год, то мне будет целый век». Сколько
лет дедушке?
3.
На каждой из двух прямых отметили по
четыре точки. Укажите наибольшее
количество треугольников с вершинами
в этих точках? Ответ обосновать.
4.
В лесу проводился кросс. Обсуждая его
итоги, одна белка сказала: «Первое место
занял заяц, а второй была лиса». Другая
белка возразила: «Заяц занял второе
место, а лось был первым». На что филин
заметил, что в высказывании каждой
белки одна часть верная, а другая – нет.
Кто был первым, а кто вторым в кроссе?
Ответы
и решения.
6
класс
1. Ответ:
85679 85679 = 171358.
2. Ответ:
66 лет.
Решение.
Пусть дедушке х лет. Составим уравнение:
х 0,5х 1 = 100; х = 66.
3. Ответ:
48 треугольников.
Решение.
Пусть на одной отмечены точки А, В, С и
D. Количество отрезков
можно подсчитать, используя дерево
возможностей:
АВС D
/ | / | /
| / |
B C D A C DAB D A BC
Отрезки
АВ и ВА совпадают и т.д. Т.о., на одной
прямой 6 отрезков, на другой 4 точки,
всего 24 треугольника. Аналогично ещё
24 треугольника.
4.
Ответ: Лиса заняла второе место, а лось
– первое.
Решение
Запишем коротко высказывания двух
белок:
1-я
белка: «Заяц – I», «Лиса – II».
2-я
белка: «Заяц – II», «Лось – I».
Если
предположить, что высказывание «Заяц
– I» верно, то оба высказывания 2-й белки
будут неверными, а это противоречит
условию задачи. Значит, высказывание
«Заяц – I» не может быть верным, тогда
Лиса заняла второе место, а Лось – первое.
7
класс
Задания
1.
Трёхзначное число на 125% больше двузначного
числа, составленного из его двух последних
цифр. Найдите это трёхзначное число.
2.
Школа Пифагора. Тиран острова Самос
Поликрат однажды спросил у Пифагора,
сколько у того учеников. “Охотно скажу
тебе, о Поликрат, – отвечал Пифагор. –
Половина моих учеников изучает прекрасную
математику, четверть исследует тайны
вечной природы, седьмая часть молча
упражняет силу духа, храня в сердце
учение. Добавь ещё к ним трех юношей, из
которых Теон превосходит прочих своими
способностями. Столько учеников веду
я к рождению вечной истины”.
Сколько учеников ведёт к рождению
вечной истины Пифагор?
3.
К числу 10 припишите слева и справа по
одной цифре так, чтобы полученное число
делилось на 72.
4.Разрежьте
квадрат на 5 прямоугольников так, чтобы
два прямоугольника не имели бы более
одной общей вершины
5.
В трёх ящиках лежат орехи. В первом ящике
на 6 кг орехов меньше, чем в двух других
вместе. А во втором – на 10 кг меньше, чем
в двух других вместе.
Сколько
орехов в третьем ящике?
Ответы
и решения.
7
класс
1.
Ответ: 180.
Решение.
100% 125%=225%, 225% =9/4 двузначного числа. Т.е.
двузначное число должно делиться на 4,
а при умножении на 9 частного от деления
должно получаться трёхзначное число.
2.
Ответ: 28.
Решение.
Пусть у Пифагора было х учеников. Составим
и решим уравнение:
х/2
х/4 х/7 3 = х
14х 7х 4х 84=28х
3х=84
х=28.
3.Ответ: 4104.
Решение.
72 – произведение чисел 8 и 9.Используя
признак делимости на 8, справа приписываем
цифру 4, по признаку делимости на 9 слева
приписываем цифру 4.
4. Ответ:

5.Ответ: 8 кг орехов
Решение.
Соединим оба заданных условия и получим
следующее утверждение: «В первом и
втором ящиках орехов на 6 кг 10 кг меньше,
чем в первом, втором и двух третьих».
Отсюда следует, что в двух третьих ящиках
16 кг орехов, то есть в третьем 8 кг орехов.
8
класс
Задания
1.У первоклассника
Феди в кассе цифр есть только единицы,
шестёрки, четвёрки и девятки. Он составил
из них 2 числа. Может ли одно них быть
ровно в 17 раз больше другого? (ответ
обосновать)
2.
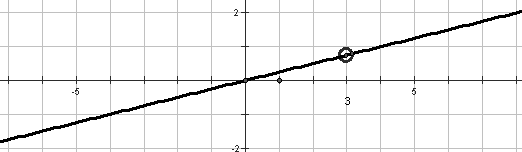
Постройте график функции
![]()
3.
Сократите дробь
а4 –
b4
64 –16 а2
(а b)2 –
8 – 2аb
и
найдите её значение при а = 37 и в = 27, не
прибегая к письменным вычислениям.
4.
Найдите углы прямоугольного треугольника,
если угол между биссектрисой и высотой,
проведёнными из вершины прямого угла,
равен 15О.
5.
Пришел Иван-царевич в подземелье к Кащею
Бессмертному Василису Прекрасную
освобождать. В подземелье 3 темницы. В
одной из них томится Василиса, в другой
расположился Змей Горыныч, а третья
темница пустая. На дверях есть надписи.
но все они ложные. На первой темнице
написано «Здесь Василиса Прекрасная»;
на второй темнице «Темница № 3 не пустая»,
на третьей темнице написано «Здесь Змей
Горыныч». В кой же темнице Василиса?
8
класс
Ответы
и решения
1. Ответ:
не может.
Решение.
У Феди есть только 1, 4, 6, 9. Если число а
заканчивается на 1, 4, 6, 9, то произведение
числа а на 17 заканчивается на
7, 8, 2, 3. А таких цифр в кассе нет.
2.
Ответ: прямая у = 0,25 х , с выколотой точкой
(3; 0,75).
Решение.
После преобразования получаем функцию
у = 0,25 х,
при
х Є (-∞; 3 ) U (3; ∞ ).
3. Ответ:а2 –
8 – b2; 632.
Решение
Числитель: а4 –
b4 64 –16 а2 =
( а4– 16 а2
64 ) – b4 =
(а2 – 8)2 –(
b2)2
= (а2 – 8 –
b2) (а2
– 8 b2).
Знаменатель: (а b)2
– 8 – 2аb = а2 2аb
b2 – 8 – 2аb = а2
b2 – 8.
а2
– 8 – b2 = (а – b) (a
b) – 8 = (37–27) (37 27) – 8 =
632.
4. Ответ:
30О, 60О, 90О.
Решение.
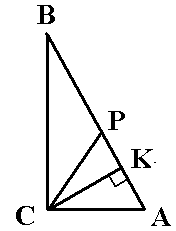
Угол
РСА равен 45О, т.к. СР биссектриса
прямого угла.Угол
КСА равен 30О (45О – 15О
= 30О).Угол
КАС равен 60О (из прямоугольного
треугольника прямоугольного АСК).Угол
СВА равен 30О (из прямоугольного
треугольника прямоугольного АВС).
5.
Ответ: во второй темнице.
Решение.
Василиса не может быть в первой темнице,
значит, она во второй или третьей темнице.
Так как третья темница пустая, Василиса
будет во второй темнице.
9
класс
1.
К числу 10 припишите слева и справа по
одной цифре так, чтобы полученное число
делилось на 72.
2.
Известно, что 1/х1 1/х2 = 0,5,
где х1 и х2 – корни уравнения
х2 х b= 0. Найдите b.
3.
В прямоугольный треугольник с катетами
2см и 6см вписан квадрат, имеющий с
треугольником общий прямой угол. Найдите
периметр квадрата.
4. Автомобиль
едет сначала 2 мин с горы, а затем 6 мин
в гору. Обратный путь он проделывает за
13 мин. Во сколько раз скорость автомобиля
при движении с горы больше, чем скорость
при движении· в гору? (Считайте, что
скорость при движении с горы (в гору)
одинакова в обоих направлениях.)
5. В трех
урнах лежат шары: в одной – два белых,
в другой – два черных, в третьей – белый
и черный. На урнах висят таблички: ББ,
ЧЧ и БЧ так, что содержимое каждой из
урн не соответствует табличке. Как,
вытащив один шар, определить, в какой
урне какие шары лежат?
9
класс
Ответы
и решения
Ответ:
4104.
Решение.
72 – произведение чисел 8 и 9.Используя
признак делимости на 8, справа приписываем
цифру 4, по признаку делимости на 9 слева
приписываем цифру 4.
Ответ:
-2.
Решение.
По теореме Виета х1 х2 = –
1 и х1* х 2 = b.
После преобразования выражения 1/х1
1/х2 = 0,5, имеем 2(х1 х2
) = х1* х 2.
Решаем
уравнение: 2 * (-1) = b,
b = – 2.
3.
Ответ: 6 см.
Решение.
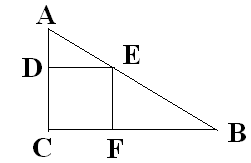
Обозначим
сторону квадрата за х. Треугольники
ADE и EFB
подобны по двум углам, отсюда имеем: (2
– х): х = х: (6 – х). Решив уравнение, получим
х = 1,5(см). Р = 6* 1,5 =6 (см).
4. Ответ:
6.
Решение.Пусть скорость
автомобиля при движении с горы равна х
км/мин, а при
движении в гору – у
км/мин. Тогда на
пути туда автомобиль едет с горы с горы
2х км,
а в гору – 6у км.
На обратном
пути расстояние 6у км (т.е. путь с горы)
автомобиль преодолевает за . 6у /х мин,
а расстояние 2х км (т.е. путь в гору) – за
2х/у мин. Всего обратный путь занимает
13 мин. Получаем уравнение:
6у
/х 2х/у = 13.
Из этого уравнения нужно найти
отношение х/у. Введя замену х/у = t, получим
уравнение с одной переменной: 2t 6/t = 13.
Решив его, найдем, t1= 6, t2 =
0,5. Так как скорость автомобиля при
движении с горы больше, чем при движении
в гору, то подходит только корень t1=
6 Таким образом, х/у = 6.
5.
Решение. Вытащим шар из урны с надписью
БЧ.
Если вытащенный
шар окажется белым, то в этой урне лежат
два белых шара, в урне с надписью ББ не
может быть белого и черного шаров,
поскольку при этом в урне с надписью ЧЧ
содержимое совпадает с надписью. Делаем
вывод о том, что в урне с надписью ББ
лежат два черных шара, а в урне с надписью
ЧЧ лежат два шара разных.
Если вытащенный
шар окажется черным, то в урне с надписью
БЧ лежат два черных шара, в урне с надписью
ЧЧ лежат два белых шара, а в урне с
надписью ББ лежат два шара разных цветов.


